Graf spójny
Graf spójny – graf, w którym każdą parę wierzchołków łączy pewna ścieżka[1]. Graf nieposiadający powyższej własności to graf niespójny[potrzebny przypis].
Warunkiem koniecznym, by graf skierowany był spójny, jest spójność jego grafu podstawowego (tego samego grafu bez kierunków na krawędziach)[1].
Spójne składowe
[edytuj | edytuj kod]Maksymalny, w sensie inkluzji, spójny podgraf grafu nazywa się spójną składową. Liczba spójnych składowych grafu G oznacza się przez
Inaczej, spójną składową grafu G jest jego spójny podgraf nie zawarty w większym podgrafie spójnym grafu G.
Nieformalnie, spójna składowa grafu jest to taki podgraf, który można ‘wydzielić’ z całego grafu bez usuwania krawędzi. Graf spójny ma jedną spójna składową. Dla przykładu, w lesie spójnymi składowymi są drzewa. Spójna składowa to fragment grafu, który nie jest połączony z innym fragmentem.
- oznacza, że graf G jest spójny,
- oznacza, że G składa się z izolowanych wierzchołków.
Wierzchołek v nazywa się rozspajającym graf G (przegubem lub punktem artykulacji w grafie G), jeżeli usunięcie v z G (wraz z przyległymi do niego krawędziami) powoduje zwiększenie (czyli jeśli po usunięciu v wraz z przyległymi do niego krawędziami, graf G ma więcej składowych niż wcześniej).
Przykład
[edytuj | edytuj kod]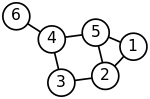
Graf ten jest spójny, więc zgodnie z definicją ma jedną spójną składową.
Po usunięciu krawędzi 2-3 i 4-5 graf ten nie jest już spójny, składa się wtedy z dwóch oddzielnych zbiorów wierzchołków:
Każdy z tych zbiorów jest spójną składową grafu, a więc łącznie cały graf posiada dwie spójne składowe –
Zobacz też
[edytuj | edytuj kod]Przypisy
[edytuj | edytuj kod]- ↑ a b graf, [w:] Encyklopedia PWN [online], Wydawnictwo Naukowe PWN [dostęp 2022-03-10].










